In the landscape of modern engineering, the proportional integral derivative control system is the most widely adopted algorithm for industrial feedback control. Whether you are looking for a pid proportional integral derivative tutorial or designing a complex proportional integral and derivative architecture for a chemical plant, understanding these three components is essential for system stability and efficiency.
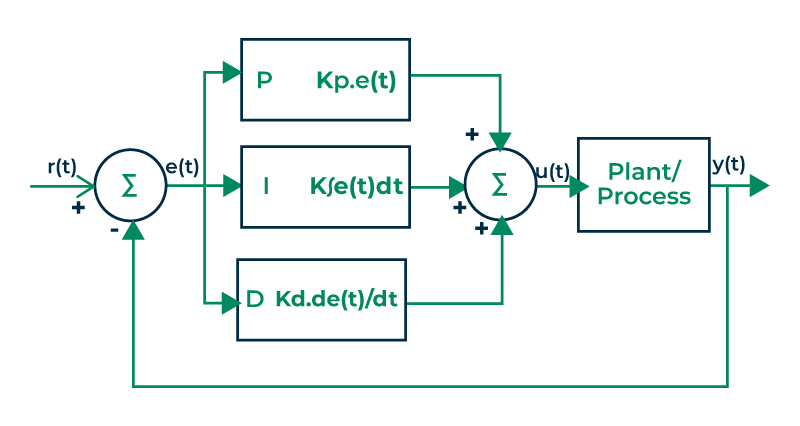
Table of Contents
Toggle1. What is a Proportional Integral Derivative Control System?
A proportional integral derivative control system is a mechanism that calculates an “error” value as the difference between a measured process variable and a desired setpoint. The controller attempts to minimize the error by adjusting the process control inputs.
2. The Mechanics: P, I, and D Explained
To achieve a perfect balance in a proportional derivative integral loop, the controller applies three distinct parameters:
Proportional (P) Control
The “P” accounts for present values of the error. If the error is large, the control output is proportionately large. While it provides the initial “kick” to move the system, P-control alone often results in an offset.
Integral (I) Control
The “I” accounts for past values of the error. It integrates the error over time, ensuring that even a small persistent deviation is eventually corrected. This is the key to eliminating steady-state errors in a proportional integral derivative loop.
Derivative (D) Control
The derivative control system acts as a “predictive” component. It estimates the future trend of the error based on its current rate of change. By providing a damping effect, it prevents the system from overshooting its target.
3. Why the “Proportional Integral and Derivative” Synergy Matters
Individually, these controllers have flaws. But as a unified proportional integral derivative system, they provide:
Rapid Response: Via the Proportional term.
Zero Offset: Via the Integral term.
Stability and Smoothness: Via the Derivative term.
In a derivative control system, the D-term is particularly vital for processes that react slowly, such as large-scale temperature control in industrial furnaces, where predicting the “thermal inertia” is the difference between success and a melted batch.
4. Industrial Applications: From Valves to Robotics
The high search volume for proportional integral derivative terms reflects its dominance in critical sectors:
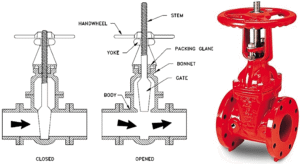
Fluid Dynamics: Controlling the opening of a high-pressure valve to maintain a precise flow rate.
Thermal Management: Managing heating elements to keep a chemical reactor at an exact temperature.
Motion Control: In robotics, the proportional derivative integral logic ensures that a robotic arm moves to a specific coordinate with millimeter precision without shaking.
5. Tuning Your Proportional Integral Derivative Loop
Tuning is the process of finding the optimal values for Kp, Ki, and Kd. Most engineers use the Ziegler-Nichols method to calibrate their proportional integral and derivative controllers.
Start with P only: Increase Kp until the system starts to oscillate.
Add I: Decrease the integral time until the offset disappears.
Refine with D: Increase the derivative gain to smooth out the oscillations.
Conclusion: The Enduring Power of PID
The proportional integral derivative control system remains the backbone of automation because it mirrors how humans make decisions: we react to the present, remember the past, and anticipate the future. For any engineer, mastering the pid proportional integral derivative logic is the first step toward building a truly “smart” system.