In servo-hydraulic actuator systems consisting of servo valves and hydraulic cylinders, proper component selection is critical for optimal performance. A fundamental design principle states that the hydraulic cylinder’s load pressure should be approximately 2/3 (or 67%) of the servo valve’s rated working pressure. Alternatively expressed: the servo valve’s inlet working pressure should be 1.5 times the load pressure differential.
This article explores the theoretical foundation of this ratio, its practical implications, and when deviations from this standard might be appropriate.
Table of Contents
ToggleThe Design Convention
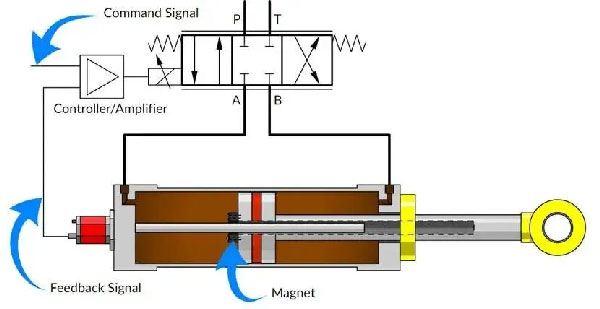
When designing servo-hydraulic systems with determined load requirements and cylinder working areas, engineers typically follow this guideline:
Servo valve selection: The inlet working pressure of the servo valve (system’s rated working pressure) should be selected at 1.5 times the load pressure difference.
Or equivalently: When calculating load capacity, the hydraulic cylinder pressure differential should be selected as 2/3 of the servo valve’s inlet working pressure.
Mathematically expressed:
δp_load = (2/3) × P_systemWhere:
- δp_load = Load pressure differential across the cylinder
- P_system = Servo valve rated working pressure (system pressure)
Theoretical Foundation
System Power Output
Consider a servo valve-hydraulic cylinder actuator system where:
- Load force: F
- Piston rod velocity: V
- System output power: P_out = F × V
In hydraulic terms:
- Load force F is proportional to pressure differential δp
- Load velocity V is proportional to flow rate Q
Therefore, the system output power can be expressed as:
P_out = δp × QWhere Q is the servo valve’s output flow rate.
Flow Rate Calculation
The servo valve flow rate can be estimated using the standard orifice flow equation:
Q = C × A × √(Δp)Where:
- C = Flow coefficient
- A = Valve opening area
- Δp = Pressure drop across the valve
Pressure Drop Analysis
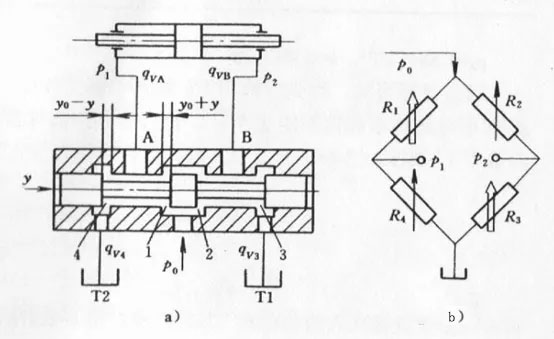
The servo valve’s main spool throttling circuit operates as a full-bridge (Wheatstone bridge) configuration. In this arrangement, oil flows through the valve’s throttling edges twice during operation:
- Once when supplying the hydraulic cylinder
- Once when oil returns from the hydraulic cylinder
Assuming:
- Symmetrical main spool design
- Zero system back pressure
- Equal pressure drop Δp at each throttling point
The pressure relationship becomes:
P_system = δp + 2ΔpWhere:
- P_system = Servo valve inlet pressure (system pressure)
- δp = Load pressure differential
- Δp = Pressure drop across each throttling edge
Solving for Δp:
Δp = (P_system - δp) / 2Optimizing for Maximum Power
The servo valve output flow rate can now be expressed as:
Q = C × A × √[(P_system - δp) / 2]The system output power becomes:
P_out = δp × Q = δp × C × A × √[(P_system - δp) / 2]To find the maximum power output, we differentiate with respect to δp and set the derivative to zero:
dP_out/dδp = 0This yields:
C × A × √[(P_system - δp) / 2] + δp × C × A × (-1) / [2√(2(P_system - δp))] = 0Simplifying:
√[(P_system - δp) / 2] = δp / [2√(2(P_system - δp))]Further simplification leads to:
2(P_system - δp) = δp
2P_system - 2δp = δp
2P_system = 3δpTherefore:
δp = (2/3) × P_systemPhysical Interpretation
This 2/3 ratio represents the optimal pressure distribution for maximum power transfer in the servo-hydraulic system. At this operating point:
- 67% of system pressure is used for useful work (driving the load)
- 33% of system pressure is consumed in valve throttling losses (16.5% per throttling edge)
This distribution ensures the best balance between available force (pressure) and achievable velocity (flow) for maximum power output.
My Technical Analysis
The derivation presented is mathematically sound and represents a fundamental optimization principle. However, several practical considerations warrant discussion:
1. Assumptions and Real-World Conditions
The theoretical model assumes:
- Perfectly symmetrical valve design
- Negligible back pressure
- Ideal flow conditions without turbulence
- Constant flow coefficient C
In practice, these assumptions may not hold perfectly, but the 2/3 ratio remains a robust guideline.
2. Energy Efficiency Perspective
Operating at the 2/3 ratio means approximately 33% of input hydraulic power is dissipated as heat through throttling losses. This represents the thermodynamic cost of achieving maximum mechanical power output. From an energy efficiency standpoint, this may not always be optimal, particularly in applications where duty cycle or energy costs are critical.
3. Dynamic Response Considerations
The 2/3 ratio optimization focuses on steady-state power. However, servo systems often prioritize dynamic response, bandwidth, and positioning accuracy. The pressure margin (the remaining 33%) provides:
- Headroom for acceleration/deceleration
- Compensation for pressure transients
- Improved control authority
- Better system damping characteristics
When to Deviate from the 2/3 Ratio
The 2/3 principle is derived for maximum power conditions, but not all applications require operation at maximum power. Consider these scenarios:
1. Force-Dominant Applications
When to use higher ratios (e.g., 4/5 or 80%):
- Applications requiring maximum force with lower speed requirements
- Press operations, clamping systems
- High-force positioning applications
Trade-offs:
- Reduced maximum velocity
- Lower power output
- Requires adequate servo valve flow margin to compensate
Example: If you need maximum clamping force but speed is secondary, operating at δp = 0.8 × P_system sacrifices only about 15% of maximum power while increasing available force by 20%.
2. Speed-Dominant Applications
When to use lower ratios (e.g., 1/2 or 50%):
- Rapid positioning systems
- High-speed pick-and-place operations
- Applications prioritizing speed over force
Trade-offs:
- Reduced available force
- Higher flow requirements
- Increased throttling losses
3. Energy-Efficiency Priority
For systems where energy consumption is critical:
- Consider variable pressure systems
- Implement load-sensing controls
- Use pump displacement control instead of throttling
- Operate at lower pressure ratios during light-load conditions
4. Control Performance Requirements
High-bandwidth servo systems may benefit from additional pressure margin (lower δp ratio) to:
- Improve control stiffness
- Enhance disturbance rejection
- Increase system damping
- Extend servo valve operating range
Practical Design Guidelines
Step 1: Determine System Requirements
- Maximum load force required
- Maximum velocity required
- Duty cycle and power profile
- Control bandwidth requirements
Step 2: Calculate Required Power
P_required = F_max × V_maxStep 3: Select Cylinder Size
Based on force requirements:
A_cylinder = F_max / (δp × η)Where η accounts for efficiency losses.
Step 4: Determine System Pressure
Using the 2/3 ratio as baseline:
P_system = 1.5 × δp_loadAdjust based on application priorities:
- For maximum force: P_system = 1.25 × δp_load (4/5 ratio)
- For maximum power: P_system = 1.5 × δp_load (2/3 ratio)
- For maximum speed/control: P_system = 2.0 × δp_load (1/2 ratio)
Step 5: Select Servo Valve
Calculate required flow at maximum velocity:
Q_required = A_cylinder × V_max / η_vSelect servo valve with:
- Rated pressure ≥ P_system
- Rated flow ≥ Q_required with adequate margin (typically 20-30%)
Validation Example
Given:
- Load force: 10,000 N
- Maximum velocity: 0.5 m/s
- Cylinder area: 0.001 m² (10 cm²)
Calculations:
- Load pressure differential:
δp = F / A = 10,000 / 0.001 = 10 MPa- System pressure (2/3 ratio):
P_system = 1.5 × 10 = 15 MPa- Required flow:
Q = A × V = 0.001 × 0.5 = 0.0005 m³/s = 30 L/min- Output power:
P_out = δp × Q = 10 MPa × 30 L/min = 5 kWServo valve selection: Choose a valve rated for 15-20 MPa system pressure with 35-40 L/min flow capacity (including margin).
Conclusion
The 2/3 pressure ratio principle represents a fundamental optimization for maximum power transfer in servo-hydraulic systems. It is derived from rigorous mathematical analysis and provides an excellent starting point for system design.
However, this ratio should not be considered mandatory. Engineers should evaluate their specific application requirements:
- Use 2/3 ratio for balanced power, general-purpose applications
- Increase the ratio (→ 4/5) for force-critical applications
- Decrease the ratio (→ 1/2) for speed-critical or high-bandwidth control applications
The key is understanding that this ratio represents a power optimization point, and deviations should be made consciously based on specific performance requirements, energy efficiency considerations, and system dynamics.
Final Recommendation: Start design calculations with the 2/3 ratio, then adjust based on application-specific priorities while ensuring adequate servo valve flow margin and pressure headroom for dynamic response and control performance.
Additional Considerations
System Efficiency
Total system efficiency includes:
- Pump efficiency (90-95%)
- Valve throttling efficiency (67% at 2/3 ratio)
- Cylinder mechanical efficiency (95-98%)
- Piping and fitting losses (2-5%)
Overall efficiency at 2/3 ratio ≈ 57-62%
Thermal Management
Operating at 2/3 ratio generates significant heat (33% of hydraulic power). Ensure adequate:
- Reservoir sizing (3-5 times pump flow rate capacity)
- Heat exchanger capacity
- Oil cooling provisions
Safety Margins
Always include safety factors:
- Pressure: 1.3-1.5× calculated pressure
- Flow: 1.2-1.3× calculated flow
- Power: 1.2× calculated power
These margins account for:
- Friction and seal wear over time
- Pressure transients
- Temperature variations
- Component tolerance variations